Finite Elemente Methode [FEM] – Einfach erklärt!
Die Finite Elemente Methode oder kurz FEM ist eines der größten Hilfsmittel für den modernen Techniker, Ingenieur oder ambitionierten Maker.
Bestimmt hast du dir schon mal beim Entwurf oder der Konstruktionen von eigenen Bauteilen eine der folgenden Fragen gestellt:
Ist mein Bauteil ausreichend stark dimensioniert?
Kann ich noch Material einsparen?
Warum vibriert meine Maschine plötzlich?
Wie kann ich leichter bauen?
Wie lange hält mein Bauteil?
Mit dem Hilfsmittel der Finite Elemente Methode kannst du diese und viele weitere Fragen beantworten!
In diesem Artikel widmen wir uns diesem „magischen“ Tool und klären die wichtigsten Fragen:
- Was ist FEM eigentlich?
- Wie funktioniert FEM? (Eine anschauliche und verständliche Erklärung)
Der Artikel ersetzt keine wissenschaftliche Erklärung der Methode, sondern versucht, sich dem Thema auf anschauliche Weise zu nähern. Ganz nach dem Motto von Albert Einstein:
Wenn du es nicht einfach erklären kannst, hast du es nicht gut genug verstanden.
Albert Einstein
Lass uns also anfangen und die „Magie“ der FEM verstehen!
Inhaltsverzeichnis
Definition Finite Elemente Methode (FEM): Was ist FEM?
Eine allgemein gültige Definition zu finden ist schwierig, da FEM vieles gleichzeitig ist. Ganz allgemein würde ich folgende Definition vorschlagen:
Die Finite Elemente Methode (FEM), oder auch Finite Elemente Analyse (FEA) genannt, ist ein numerisches Verfahren zur Lösung von physikalischen Problemen. Dabei wird das Berechnungsgebiet in endliche (finite) Teile zerlegt, und die Differentialgleichungen des physikalischen Problems gelöst.
Zugegeben, die Definition ist etwas kryptisch und enthält einige mathematische Fachbegriffe. Versuchen wir daher einen anderen Ansatz, um zu verstehen, was FEM genau ist. Aber Achtung, jetzt wird es unwissenschaftlich 😉 :
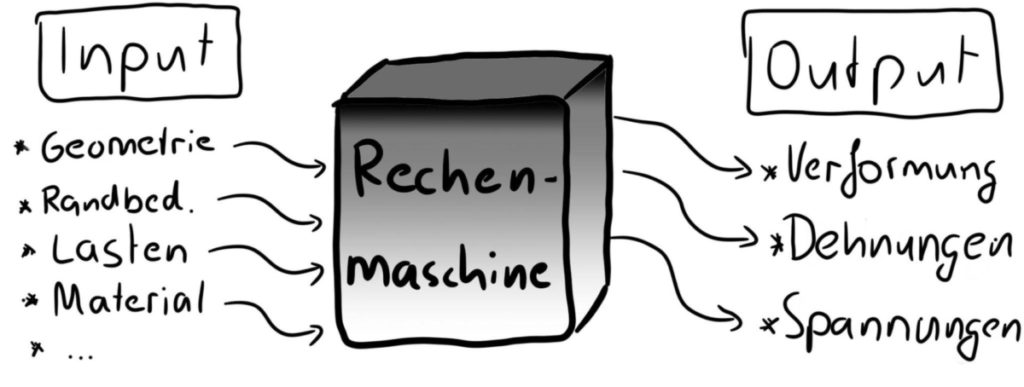
In erster Linie kannst du dir die FEM als eine Art Rechenmaschine vorstellen. Du fütterst die Rechenmaschine mit Informationen, und anschließend berechnet sie dir ein Ergebnis. Das Ergebnis kannst du dir dann anzeigen lassen. So einfach ist das. 🙂
Wie die Rechenmaschine im Innersten funktioniert, schauen wir uns in einem späteren Kapitel an.
Was kann ich mit FEM berechnen?
Die tolle Rechenmaschine, in Form eines magischen schwarzen Kastens, kann einiges für uns tun:
Wir können damit Probleme der Strukturmechanik (Statik, Dynamik), der Wärmeübertragung, der Akustik und sogar elektrische und elektromagnetische Fragestellungen lösen.
Bezugnehmend zur Einleitung beschränke ich mich in diesem allgemeinen Artikel auf die Probleme der Strukturmechanik, genauer auf die am weitesten verbreitete Berechnungsart: die lineare Statik! Die prinzipielle Vorgehensweise der vielen anderen physikalischen Disziplinen ist jedoch ähnlich.
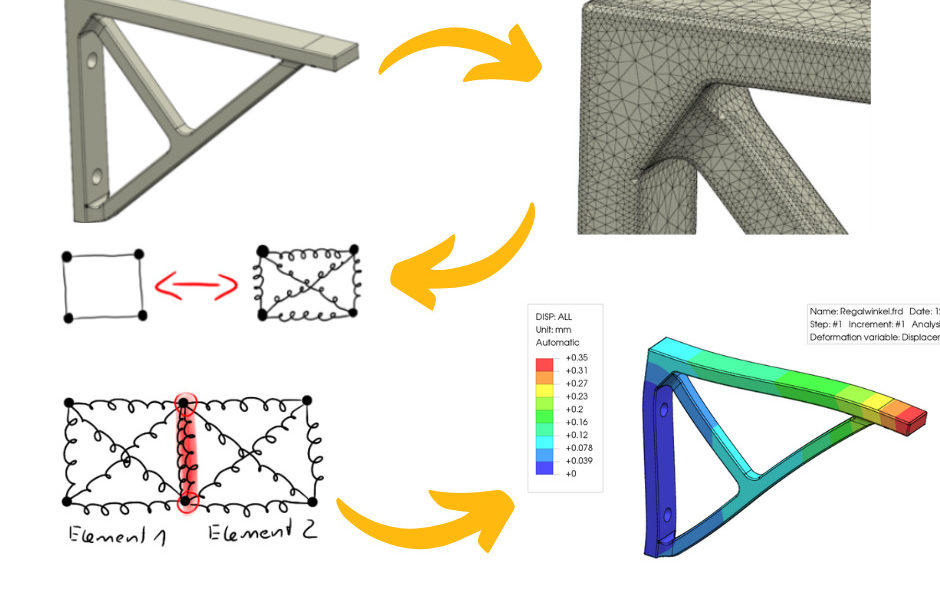
Um das anschauliche Modell des magischen schwarzen Rechenkastens weiter zu verfolgen, betrachten wir nun ein einfaches Problem: Du hast einen Metallwinkel vorliegen, und möchtest wissen, ob dieser eine bestimmte Last aushält oder nicht.
Obwohl die Geometrie relativ einfach ist, kannst du für die Lösung keine „fertige“ Formel verwenden. Man spricht auch von geschlossenen Lösungen. Nur in den seltensten Fällen (bei sehr einfachen Problemen) liegen diese vor. In der Praxis ist daher meist eine numerische Näherungslösung notwendig (FEM).
Du musst nun den schwarzen Rechenkasten mit Informationen füttern, damit er für dich das Problem lösen kann.
Randbedingungen der Finite Elemente Methode
Zunächst benötigt unser Rechenkasten Geometrieinformationen: Wie sieht der Winkel genau aus? Welche Dicke hat er und aus welchem Material besteht er? Kurz gesagt: Du benötigst ein 3D-Modell bzw. CAD-Modell des Metallwinkels.
Weiterhin musst du festlegen, welche maximale Last auf dem Winkel liegen soll, und wo er an der Wand befestigt wird.
Jetzt wird es langsam spannend. Du musst dem schwarzen Kasten nämlich auch sagen, welche physikalischen Modelle er zur Berechnung heranziehen soll. Bei unserem einfachen Problem ist erstmal klar, dass es sich um eine statische Berechnung handelt. Komplizierter wird es schon beim Materialmodell. Soll unser magischer schwarzer Kasten ein lineares oder nichtlineares Materialmodell wählen?
So langsam merkst du vielleicht: die Rechenmaschine benötigt einige Informationen.
Wie wichtig sind die Randbedingungen einer FEM-Simulation?
Und somit sind wir schon an einem, wenn nicht gar dem wichtigsten, Knackpunkt von FEM-Simulationen angelangt:
Das FEM-Programm liefert dir immer ein Ergebnis. Ob dieses korrekt ist, hängt aber maßgeblich von den vorgegebenen Randbedingungen ab!
Viele Anwender fragen sich, ob man die Mathematik hinter der FEM verstehen muss? An der Uni wird der Fokus in der Regel auf die Herleitung der Differentialgleichungen gelegt. Der praktische Aspekt kommt dabei oft zu kurz – dabei ist dieser am Wichtigsten! Was nützt dir das perfekte FEM-Modell, bei dem du die Mathematik dahinter herleiten kannst, wenn du die falschen Randbedingungen setzt?
Die Antwort ist kurz: GAR NICHTS! Weil dein Ergebnis unter Umständen falsch ist! Um gute FEM-Berechnungen durchzuführen, solltest du verstehen was du tust, und welche Randbedingungen für das Problem geeignet sind.
Halten wir also bis hierhin fest: Die Eingabedaten bzw. Randbedingungen der FEM-Berechnung sind für das spätere Ergebnis essenziell, und zählen zu den wichtigsten Schritten bei der Durchführung!
Die schwierige Aufgabe besteht also immer darin, ein reales Problem so zu vereinfachen, dass das Berechnungsmodell dennoch ausreichend genaue Ergebnisse liefert.
Die Ergebnisse der FEM-Berechnung
Unser schwarzer Rechenkasten hat mit den eingegebenen Daten eine Berechnung durchgeführt. In unserem Beispiel mit den Regalwinkeln spuckt er nun verschiedene physikalische Größen aus. In der Regel kannst du dir die Verformungen, Dehnungen und Spannungen an jeder beliebigen Stelle deiner Geometrie anschauen:
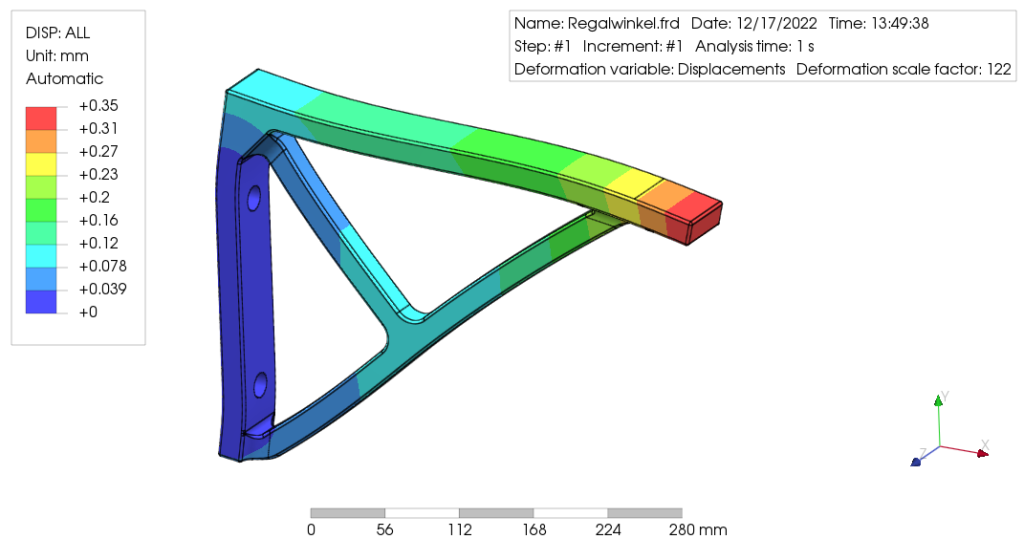
Ich nenne das: Ergebnisse erzeugen! Die anfängliche Frage, ob der Regalwinkel unter der Last hält oder nicht, wird erstmal nicht direkt beantwortet.
Das musst du nämlich selbst tun: Ergebnisse interpretieren und analysieren. Dieser Schritt ist deutlich schwerer, dies nimmt uns die Rechenmaschine nicht ab!
Erst mit der Analyse der erzeugten Ergebnisse kann die Frage beantwortet werden, ob das Bauteil hält oder nicht.
Die Interpretation ist für mich das Zweitwichtigste, nach dem Setzen der Randbedingungen!
Im Folgenden widmen wir uns schließlich der Funktionsweise der FEM. Wie funktioniert die Magie dahinter? Sei gespannt, ich versuche auch auf große Mathematik zu verzichten. (Die Herleitung von Differentialgleichungen ist nämlich absolut nicht meine Stärke 🙂 )
Wie funktioniert die Finite Elemente Methode? Eine verständliche Erklärung!
Kommen wir nun zum Inneren des magischen Rechenkastens. Und klären: Wie funktioniert die Finite Elemente Methode?
Übersetzt bedeutet „finite“ endlich. Also könnte man auch sagen: „endliche Teile“.
Die vorgegebene CAD-Geometrie muss zunächst in viele (endliche) Teile zerlegt werden. Ganz vereinfacht gesprochen muss die CAD-Geometrie in viele kleine Stücke zerhackt werden.
Dieser Vorgang nennt sich Vernetzen. Dabei entsteht ein Rechennetz, im Englischen auch „Mesh“ genannt.
Beim „Zerhacken“ der Geometrie musst du jedoch einiges beachten, bzw. kannst du nicht einfach das virtuelle Beil rausholen und die Geometrie wild zerteilen. Hier solltest du bestimmte Elemente verwenden.
Schauen wir uns das etwas genauer an.
Rechennetz bzw. Mesh: Das Rückgrat jeder FEM-Berechnung
Das Rechennetz besteht aus vielen Elementen. Schauen wir uns daher zunächst die verschiedenen Elemente-Typen an.
Wir teilen in 1D-Elemente (auch Balken bzw. „Beams“ genannt), 2D-Elemente (Schalen bzw. „Shell“ genannt) und 3D-Elemente (auch „solids“ genannt) ein.
Ein 1D-Element besteht nur aus zwei Knoten, welche durch eine Linie verbunden sind:

Bei 2D-Elementen werden meistens dreieckige (TRI) oder viereckige (QUAD) Formen eingesetzt:
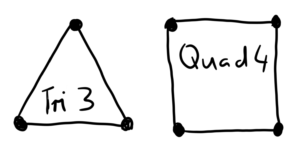
Bei den 3D-Elementen werden Tetraeder oder Hexaeder verwendet.
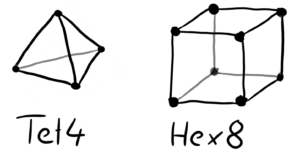
Es gibt noch weitere Elemente. Die hier gezeigten geben einen ersten soliden Überblick über die Thematik. Bei den hier dargestellten Elementen besitzen nur alle Eckpunkte einen Knoten: Es handelt sich um lineare Elemente. Daneben gibt es noch Elemente höherer Ordnung. Diese haben einfach mehr Knoten, welche mittig auf den Verbindungslinien liegen.
Zurück zu unserem Problem mit dem Metallwinkel: Die vorliegende CAD-Geometrie muss also in endliche Elemente zerlegt werden (man spricht auch von Diskretisieren der Geometrie!). Keine Angst, diese Arbeit übernimmt eine Software. Allerdings musst du als Nutzer vorher einige Einstellungen vornehmen, und dem Vernetzungsprogramm mitteilen, wie es die Geometrie zu vernetzen hat.
Unser Metallwinkel wird mit Tetraedern (zweiter Ordnung) vernetzt. Für eine optisch bessere Darstellung werden allerdings in der Regel immer nur die Eckknoten in den jeweiligen Programmen dargestellt:
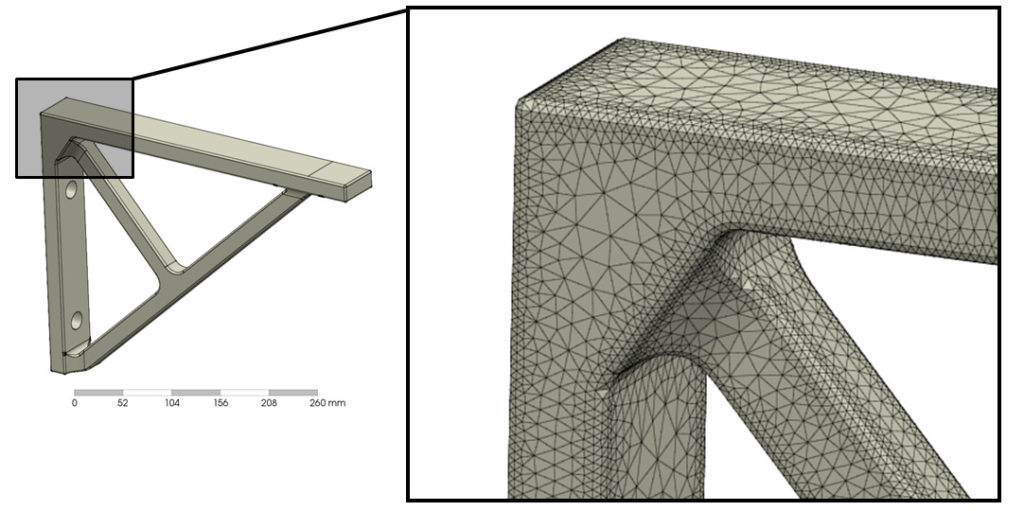
Wenn du es bis hierhin geschafft hast, wirst du dich nun bestimmt fragen: Warum brauche ich das denn? Und jetzt kommt endlich die Physik ins Spiel!
Jetzt kommt Physik ins Spiel: Elastizität und Robert Hook lassen grüßen!
Im Jahre 1678 veröffentlichte Robert Hook das nach ihm benannte Hookesche Gesetz, oder auch Gesetz der Elastizität genannt.
Hooke war wahrlich ein Genie, und seiner Zeit weit voraus. Er lag zudem im Streit mit seinem Kollegen Newton, der nach Hookes Tod sogar versuchte, sein Vermächtnis zu zerstören. Wir können froh sein, dass dies nicht gelungen ist. Denn ohne die Errungenschaften von Hooke wäre die Welt heute sicherlich nicht dieselbe. Robert Hooke ist also ein Gigant der Wissenschaft!
Das Hookesche Gesetz einfach erklärt
Im Wesentlichen besagt das Hookesche Gesetz, dass sich ein fester Körper proportional zu der auf ihn einwirkenden Kraft dehnt.
Am einfachsten lässt sich das Gesetz anhand von Federn erklären:
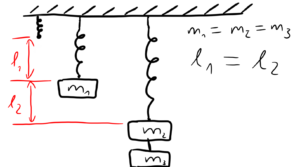
Nimmt man ein Gewicht und hängt es an eine Feder, so dehnt sich diese um einen Weg aus. Wird das Gewicht wieder entfernt, so geht die Feder wieder in ihre ursprüngliche Länge zurück. Nimmt man nun ein doppelt so schweres Gewicht und hängt es an die Feder, so dehnt sich die Feder auch doppelt so lang aus. Man spricht von einem linear-elastischen Verhalten. In Formeln ausgedrückt bedeutet das:
![]()
![]()
![]()
![]()
Verwendung der Hookeschen Federn im Element
Wie kommen wir jetzt vom Hookeschen Gesetz auf die Erklärung der FEM? Schauen wir uns hierfür ein beispielhaftes Element der FEM an. Zunächst verbinden wir die Knoten des Elements mit Federn:
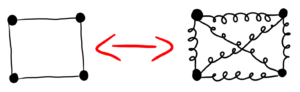
Nun können wir an den Knotenpunkten des Elements Randbedingungen anbringen oder auch Lasten auflegen. Das sieht dann für unser einzelnes Quad4-Element beispielsweise so aus:
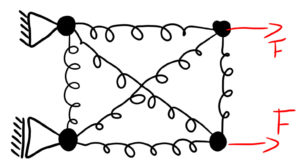
Jetzt kann man sich sehr gut vorstellen, wie sich die Federn des Elements dehnen und die Knoten verschieben. Unser Element lässt sich also, vereinfacht gesprochen, über die Hookeschen Federgleichungen beschreiben. Man spricht in der Finite Elemente Methode auch von der Formfunktion des Elements.
Um ein komplexeres Bauteil wie unseren Winkel mit Hilfe der Federn zu beschreiben, benötigen wir aber sehr sehr viele Elemente mit Federn. Die einzelnen Federgleichungen eines Elements können dabei mit dem benachbarten Element und deren Federgleichungen gekoppelt werden. Dies geschieht über die gemeinsamen Knotenpunkte. Die Verschiebung des Knotens ist also in beiden Elementen gleich. Unser gekoppeltes Federmodell sieht dann so aus:
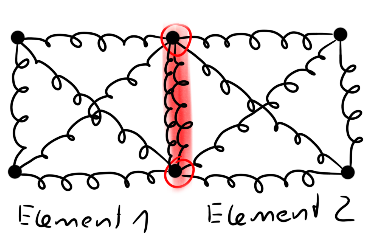
Was ist die Folge dessen?
Es kann ein (sehr großes) Gleichungssystem, mit allen zum Bauteil gehörenden Elementen, aufgestellt werden:
![]()
![]()
![]()
![]()
In dem System sind dann auch entsprechende Randbedingungen (Bsp.: Einspannung u=0 oder Lasten F) enthalten.
Das Problem des Gleichungssystems: Wir können es, aufgrund der Größe, meist nicht so einfach per Hand lösen. Wir benötigen dazu moderne Rechentechnik, also einen Computer und Software. In der FEM spricht man hier vom sogenannten Solver!
Der FEM-Solver: Das Herzstück der Finite Elemente Methode
Der FEM-Solver löst das obige Gleichungssystem, sodass für jeden Knoten die Verschiebungen u vorliegen. Grundsätzlich unterscheidet man zwischen direkten und iterativen Gleichungslösern. Auf weitere Details der Löser möchte ich aber an dieser Stelle verzichten.
Die genaue Funktionsweise moderner Solver lässt sich nur mit höherer Mathematik erklären. Hier passt die Analogie zum Auto sehr gut: Du musst nicht genau wissen, wie das Auto funktioniert. Also wie die thermodynamischen Prozesse im Motor ablaufen, oder wie das Getriebe im Detail aufgebaut ist. Um Auto zu fahren, musst du das „Handwerk“ beherrschen: Wie schaltet man richtig, welche Verkehrsregeln gibt es usw. Bei der FEM sehe ich das genauso: Du musst den Solver mathematisch nicht im Detail verstehen. Du musst aber wissen, wie du richtig „fährst“, also den Solver einsetzt!
Zurück zu unserem Problem: Der Solver berechnet also an jedem Knoten unseres Rechennetzes die Verschiebung u. Damit lassen sich auch sehr einfach die Dehnungen berechnen. Anschließend kann mit Hilfe eines Materialgesetzes die Spannung berechnet werden. Im einfachsten Fall nutzen wir hierfür ein lineares Materialgesetz:
![]()
![]()
![]()
![]()
Jetzt ist der magische Kasten fertig, und die Ergebnisse können an den entsprechenden Elementen und Knoten angezeigt werden!
Zugegeben: Die Erklärung ist sehr vereinfacht, allerdings versteht man meiner Meinung nach das Grundprinzip der Finite Elemente Methode sehr gut.
Wer an dieser Stelle noch weitere mathematische Erläuterungen bevorzugt, dem empfehle ich diese Seite von FEM-Helden. Darin wird das Federmodell aufgegriffen, und mathematisch an einem einfachen Stab die gesamte Berechnung sehr anschaulich durchgeführt!
Versteht mich also nicht falsch: Die Mathematik dahinter genau zu verstehen, ist sicherlich vorteilhaft. Aber es ist nicht Bedingung, um gute FEM-Berechnungen durchzuführen!
Zusammenfassung: Finite Elemente Methode
Fassen wir das Wichtigste noch einmal zusammen. Die Finite Elemente Methode ist ein numerisches Näherungsverfahren für die Lösung von verschiedensten physikalischen Problemstellungen.
Dabei wird die Geometrie in endliche (finite) Teile (Elemente) zerlegt, und die physikalischen Differentialgleichungen gelöst.
An unserem Beispiel der linearen Statik wird dies mit den Hookeschen Federgleichungen sehr anschaulich verdeutlicht. Die einzelnen Elemente werden dabei über Federn physikalisch beschrieben. Durch Kopplung der Elemente an den gemeinsamen Knotenpunkten, kann ein gekoppeltes Gleichungssystem aufgestellt werden.
Der FEM-Solver löst das Gleichungssystem, und stellt dir dabei die Ergebnisse an jeder beliebigen Stelle der Geometrie zur Verfügung. Bei unserem Problem der linearen Statik sind das Verformungen, Dehnungen und Spannungen. Anhand dieser Daten musst du als Anwender dann entscheiden, ob dein Bauteil hält oder nicht. Die Interpretation der Ergebnisse ist also dir als Nutzer vorbehalten!
Für die Richtigkeit der Ergebnisse ist es essenziell, die richtigen Randbedingungen zu setzen. Hier besteht die Herausforderung: Die Übertragung der Realität in ein physikalisches Modell, welches die Realität möglichst genau nachbildet. Dementsprechend sind die Ergebnisse einer FEM Simulation immer kritisch zu betrachten: Sind die Randbedingungen falsch, ist auch das Ergebnis falsch!
Ich hoffe, du hast jetzt ein besseres Verständnis der FEM und weißt, wie sie im Groben funktioniert. Auch ohne tiefgreifende mathematische Kenntnisse ist es möglich, die FEM als wichtiges Hilfsmittel in der Konstruktion einzusetzen.
Wenn du keine weiteren Artikel zum Thema FEM verpassen möchtest, abonniere sehr gern meinen Newsletter. Ich freue mich auch immer über Kommentare!
Häufig gestellte Fragen: Finite Elemente Methode (FEM)
Die Finite Elemente Methode (FEM) oder auch Finite Elemente Analyse (FEA) genannt, ist ein numerisches Verfahren zur Lösung von physikalischen Problemen. Dabei wird das Berechnungsgebiet in endliche (finite) Teile zerlegt und die Differentialgleichungen des physikalischen Problems gelöst. Erfahre mehr dazu im FEM-Artikel.
Bei der Finite Elemente Methode (kurz: FEM) wird das zu berechnende Bauteil in viele kleine Elemente eingeteilt. Die physikalischen Gesetze werden dann auf diese finiten Teilen angewandt. Dadurch lassen sich Probleme der Strukturmechanik, der Akustik und der Thermodynamik lösen. Erfahre in dem Artikel anschaulich, wie genau FEM funktioniert.
Der FEM-Solver ist das Herzstück der Finite Elemente Methode. Er löst das entstehende Gleichungssystem der physikalischen Problemstellung mit Hilfe eines direkten oder indirekten numerischen Verfahrens.
Ich bin der Meinung, dass dies nicht notwendig ist. Du musst wissen, wie FEM funktioniert, und das „Handwerk“ beherrschen. Mit Hilfe moderner Software kann dann eine FEM Simulation durchgeführt werden.
Bei der FEM handelt es sich um ein numerisches Verfahren zur Lösung von physikalischen Differentialgleichungen. Damit können Probleme der Mechanik, der Thermodynamik oder der Akustik gelöst werden. So kann die Verformung eines Bauteils unter einer vorgegebenen Last berechnet, und die Spannungen ausgewertet werden. Erfahre in diesem FEM-Artikel mehr.
Die Verwendung der richtigen Randbedingungen ist einer der wichtigsten Schritte bei einer FEM Berechnung. Das reale Problem muss mit Hilfe von Randbedingungen so vereinfacht werden, dass es trotzdem die Realität möglichst genau abbildet.

3 Comments
Es wäre für mich als Ahnungslosen vielleicht besser zu verstehen, wenn man das zu berechnende Teil aus z.B. weichen Ton beschreibt. Das Teil kann sich nach einer definierten Belastung nicht zurück formen, aber man kann sofort den Fehler im Entwurf erkennen, oder? Die Anziehungskraft mal ausser vor gelassen!
Die Beschreibung mit Ton kann meiner Meinung nach zu Missverständnissen führen. Denn bei einem für Metalle typischen linear-elastischen Werkstoffverhaltens kommt es beim Wegnehmen der Belastungen wieder zur ursprünglichen Form des Bauteils. Der Winkel verformt sich also unter der Last und wenn die Last entfernt wird, geht der Winkel wieder in seine ursprüngliche Form zurück. Erst beim Überschreiten der Dehngrenze kommt es zu bleibenden Verformungen. Man spricht dann von plastischen Verformungen.
Sehr schön erklärt. Ich kenne ein Bauwerk mit unten ovalen Leimholz-Dachträgern – also herkömmlich Träger auf zwei Stützen mit nicht kontinuierlicher Höhe. Erforderliche Breite herkömmliche Berechnung: 25cm. Berechnung mit FEM unter Berücksichtigung der exakten Geometrie: 17 cm Breite. Erhebliche Materialersparnis durch ein anderes Rechenverfahren.